What is the Slope of Mn? A Line with Points M(1, 3) and N(5, 0) Reveals the Answer!

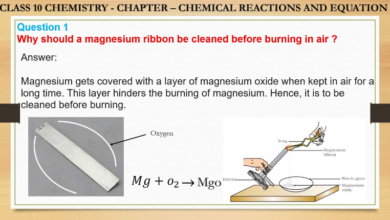
The slope of line MN containing points M(1, 3) and N(5, 0) is -3/4. The formula for slope is (change in y)/(change in x).
The slope of MN is calculated as (0 – 3)/(5 – 1) = -3/4. Understanding the slope of a line is essential in determining its steepness or direction. In this case, the points M(1, 3) and N(5, 0) help us find the slope of line MN.
By applying the formula for slope, we can determine that the slope of MN is -3/4, indicating the rate of change between the two points on the line. This fundamental concept forms the basis of analyzing and interpreting various types of linear relationships in mathematics and real-world scenarios.
Contents
Understanding Slope
To find the slope of line MN, use the formula m = (change in y)/(change in x). So, the slope of MN, between points M(1,3) and N(5,0), is equal to (0-3)/(5-1), which simplifies to -3/4. This means the line has a slope of -3/4, indicating a negative incline from M to N.
Definition Of Slope
Slope, represented by m, is the measure of the steepness of a line. It reflects how much a line rises or falls as it moves horizontally, demonstrating the rate of change along the y-axis concerning the x-axis.
Formula For Calculating Slope
The formula to calculate the slope (m) of a line passing through two points (x₁, y₁) and (x₂, y₂) is given by m = (y₂ – y₁) / (x₂ – x₁). This formula quantifies the change in the vertical coordinates (rise) divided by the change in the horizontal coordinates (run) to determine the line’s slope. The slope of the line MN, passing through points M(1, 3) and N(5, 0), can be calculated using this formula.
Plugging in the given coordinates will allow us to find the slope of the line. This method of calculating slope serves as a fundamental concept in understanding the characteristics of linear equations and their corresponding graphical representation.
Finding The Slope Of A Line
The slope of line MN, containing points M(1, 3) and N(5, 0), can be found by using the formula: slope = (change in y)/(change in x). Therefore, the slope of MN is -3/4.
Given Two Points On A Line
When presented with points M(1,3) and N(5,0) on a line, we can determine the slope of the line between these two points.
Using The Formula
To calculate the slope of the line MN, we can utilize the slope formula, which states that slope = (change in y)/(change in x).
By substituting the given coordinates of points M and N into the formula, we can easily find the slope of the line.
For points M(1,3) and N(5,0), the slope calculation would be as follows: slope = (0 – 3)/(5 – 1) = -3/4.
Application Of Slope
Slope is the measure of steepness of a line, calculated by rise over run.
Relationship Between Lines
Lines with different slopes intersect at a point, forming angles between them.
Linear Function Representation
Linear functions represent straight lines. Slope-intercept form: y = mx + b, where m is the slope.
Perpendicular Lines
Perpendicular lines have slopes that are negative reciprocals of each other. Example: If one line has a slope of 2, its perpendicular line will have a slope of -1/2.
Applying this to points M(1, 3) and N(5, 0), we can calculate the slope of line MN by:
- Find the change in y: 0 – 3 = -3
- Find the change in x: 5 – 1 = 4
Therefore, the slope of line MN is -3/4.
Conclusion
The slope of the line MN, which contains the points M(1, 3) and N(5, 0), is calculated as the change in y over the change in x, also known as rise over run. By applying the formula slope = (change in y)/(change in x), we find the slope to be -3/4.
This information allows us to determine the steepness and direction of the line.